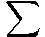BAYES'SCHE NETZE
PROBABILISTISCHE NETZE
(Bayesian Networks / Probabilistic Networks / Causal Belief Networks)
(Triangulierung)
|
Definition
trianguliert:
Ein Graph ist trianguliert wenn er keinen abkürzungsfreien zyklischen Pfad mit mehr als drei Knoten (entsprechend >3 Kanten) beinhaltet. |
|
Definition zyklisch:
Ein Pfad ist zyklisch wenn er von einem Knoten A über weitere Knoten (z.B. B, C, D) zurück zum Knoten A führt. Wobei jeder Zwischenknoten nur einmal in einem Zyklus vorkommen darf. |
|
Definition
abkürzungsfrei:
Abkürzungsfrei ist ein solcher zyklischer Pfad, wenn keine zwei Knoten dieses Pfades durch eine Kante verbunden sind, die nicht schon Teil des Pfades ist. |
Ist ein Graph nicht trianguliert so wird er durch zusätzliche Kanten, die sogenannten Fill-Ins in einen triangulierten Graphen überführt. Wie in der Einleitung bereits beschrieben gibt es verschiedene Kriterien nach denen die Güte einer Decomposition bestimmt werden kann. Das allgemeinste Kriterium ist die Tree-Width, welche durch die Anzahl der Knoten der größten (=knotenreichsten) Clique minus 1 bestimmt ist. Ein offensichtliches, aber - insbesondere während eines Suchlaufs nach einer möglichst guten Triangulierung - normalerweise aufwändiger zu berechnendes Kriterium ist die Anzahl der zusätzlich benötigten Fill-Ins. Bei der Erstellung eines Junction-Trees ist die Größe der benötigten Wahrscheinlichkeitstafeln das eigentliche Zielkriterium - da dieses aber noch aufwändiger zu berechnen ist, wird oft auf einfachere Kriterien hin optimiert, mit der (zumeist durchaus berechtigten) Hoffnung, dass der entstehende Junction-Tree auch im Hinblick auf das zuletzt genannte Kriterium relativ gut ist.
Triangulierte und nicht triangulierte Graphen
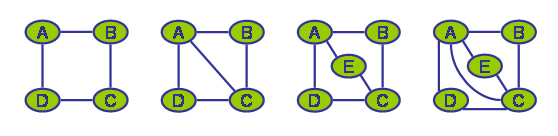
Um einen triangulierten Graphen und gleichzeitig die Cliquen zu bestimmen wird zumeist der Eliminierungs-Algorithmus benutzt. Dieser wird hier nochmals kurz dargestellt:
- Wähle einen Knoten X
- Verbinde paarweise alle Nachbarn von X durch eine Kante (wenn noch nicht verbunden)
- Sofern X und alle Nachbarn von X nicht schon Teil einer zuvor gefundenen Clique sind bilden sie eine neue Clique
- Entferne (eliminiere) X (und
damit auch alle Kanten an X)
- Wiederhole die Schritte 1-4 bis kein Knoten mehr übrig ist
Triangulierungen
Umgekehrt ist es allerdings nicht möglich alle zulässigen Triangulierungen durch eine Eliminierungsreihenfolge abzubilden. Man kann ja z.B. beliebig viele überflüssige Kanten einfügen - so ist z.B. ein vollständig verbundener Graph immer eine korrekte Triangulierung eines Ausgangsgraphen, selbst wenn dieser aus N Knoten ohne eine einzige Kanten bestünde (also vollständig unverbunden wäre). Es gibt Autoren die darauf verweisen, dass die optimale Triangulierung teilweise nicht durch eine Eliminierungsreihenfolge abgebildet werden könne. Ich habe dafür allerdings noch kein Beispiel gesehen...
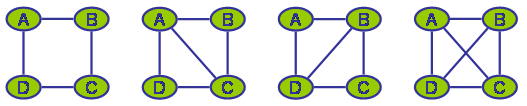
Es ist jedoch nicht besonders schwierig Beispiele zu konstruieren bei denen der oben beschriebe 1-Step-Lookahead Algorithmus nicht die optimale Triangulierung findet (siehe. Abbildung unten).
Suboptimale Lösungen mit der One-Step-Lookahead-Heuristik
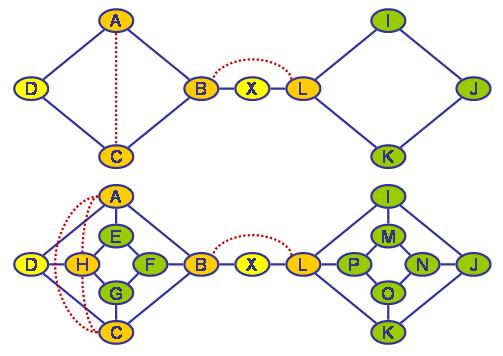
Betrachten wir noch einmal etwas allgemeiner den Eliminierungsansatz: Man kann einen Graphen G immer in zwei Teilgraphen G1 und G2 zerlegen indem man G an einer trennenden Menge von Knoten X1...Xn aufspaltet. Die trennenden Knoten X1...Xn sind dabei Teil beider Subgraphen - also sowohl in G1 als auch in G2 enthalten. Die Knoten X1...Xn müssen dabei vollständig verbunden werden, d.h. jedes noch nicht durch eine Kante verbundene Knotenpaar Xi,Xj aus X1...Xn muss durch eine Fill-In-Kante verbunden werden. Führt man dieses Verfahren rekursiv auf allen entstehenden Sub-Graphen durch, bis keine weiteren Aufspaltungen mehr möglich sind, ist garantiert, dass der Ausgangsgraph G durch alle eingefügten Fill-Ins in einen triangulierten Graph Gt überführt werden kann.
|
Definition trennende
Knotenmenge:
Eine Knotenmenge ist dann trennend wenn es keinen Pfad von einem Knoten aus G1 zu einem Knoten aus G2 gibt der nicht über (mind.) einen der trennenden Knoten X1...Xn führt |
|
Definition
vollständig verbundene
Knotenmenge:
Eine Menge von Knoten X1...Xn ist vollständig verbunden, wenn alle Paare Xi,Xj aus X1...Xn durch eine Kante Xi-Xj verbunden sind. |
Der Eliminierungsansatz ist damit ein Spezialfall dieses Verfahrens: Es wird dabei nämlich jeweils ein Sub-Graph abgespalten der nur aus genau einem Knoten X0 plus der trennenden Knotenmenge X1...Xn besteht, wobei X1...Xn natürlich genau die Nachbarn von X0 in G sind.Da der entstehende Sub-Graph für X0 durch die Fill-Ins bereits vollständig verbunden ist (X0 ist logischer Weise bereits mit all seinen Nachbarn verbunden und diese werden durch Fill-Ins vollständig verbunden, soweit dies noch nicht der Fall ist), braucht er nicht weiter aufgespalten zu werden. Im oben gezeigten Beispielgraphen könnten jeweils durch Aufspaltung am trennenden Knoten X (oder auch B oder L) zwei Teilgraphen entstehen. Solche trennenden Knotenmengen, die nur aus einem einzigen Knoten bestehen sind noch relativ leicht zu identifizieren und können als eine Optimierung in das Verfahren eingebaut werden. Leider ist dies für komplexere Knotenmengen so nicht durchführbar (jedenfalls ist mir kein effektives Verfahren bekannt).
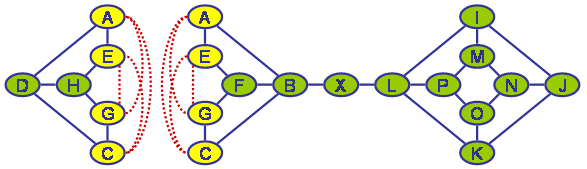
Aufspalten eines Graphen an einer trennenden Knotenmenge
Die beiden oben gezeigten Beispielgraphen legen noch eine weitere relativ einfache Optimierungsvariante nahe:
Re-compiliere einzelne Cliquen, wobei jeder Separator zu einer Nachbar-Clique im Hypertree jeweils in mindestens einer der entstehenden neuen Cliquen vollständig erhalten sein muss, damit der entstehende Sub-Hypertree anstelle der ursprünglichen Clique eingefügt werden kann. Dazu nimmt man den Sub-Graphen der nur die Knoten der gerade bearbeiteten Clique enthält und verbindet paarweise alle Knoten die einem gemeinsamen Separator angehören und führt auf diesem Sub-Graphen das oben beschriebene One-Step-Lookahead-Verfahren durch. Im oben gezeigten Beispiel würde die Clique {B, X, L} so in die Cliquen {B, X} und {X, L} aufgespalten3). Leider ist der oben gezeigte Graph da offenbar eine seltene Ausnahme, denn in allgemeinen, komplexeren Graphen führt das Verfahren praktisch nie zu einer Aufspaltung bestehender Cliquen. Normalerweise verbinden suboptimale Fill-Ins auch selten Knoten die in keinem gemeinsamen Zyklus enthalten sind. Meiner Beobachtung nach scheitert das Verfahren zumeist daran, dass durch die ein Clique verbindenden Separatoren bereits ein vollständig verbundener Sub-Graph erzwungen wird, der dann nur in einer (nämlich der bereits gefundenen) Clique aufgehen kann...
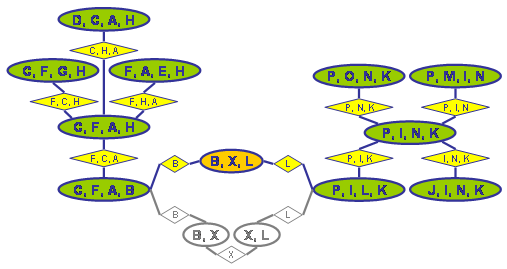
Suboptimaler vs. optimaler Hypertree
Aufwändigere Optimierungsverfahren benutzen z.B. Simulated-Annealing [3], Evolutionäre Algorithmen [2], Branch-and-Bound-Verfahren oder Ant-Colony-Optimization [1].
Hierbei ist zumeist die Eliminierungsreihenfolge (A, B, C, D, ...) der Knoten Gegenstand der Optimierung (und nicht z.B. die Menge der einzufügenden Fill-Ins).
Einige der genannten Verfahren werden im Folgenden ganz kurz vorgestellt.
Weitere Verfahren zielen darauf ab den Graphen zunächst zu vereinfachen ([4]), oder mithilfe "sicherer Separatoren" in Teilgraphen zu zerlegen ([5]), jeweils ohne die maximal entstehende Cliquen-Größe zu beeinflussen. Um tatsächlich einen Hypertree (z.B. Junction-Tree) zu erzeugen (und nicht z.B. nur die maximale Tree-Width abzuschätzen) müssen die angewendeten Vorverarbeitungsschritte natürlich reversibel sein.
Wieder andere Verfahren versuchen bereits bestehende Cliquen eines Hypertrees nachträglich in kleinere Cliquen aufzuspalten. Zumindest theoretisch lässt sich mit solchen Verfahren ein Hypertree auch komplett konstruieren, wenn man mit einem Hypertree beginnt, welcher nur eine Clique umfasst, die alle Knoten des Ausgangsgraphen enthält4).
Ant-Colony-Optimization (ACO):
Die Grundidee ist, dass sich Individuen (Ameisen) auf einer Topologie von Spots und jeweils zwei Spots verbindenden Trails bewegen5). Die Trails haben einen A-Priori-Wert, der anfänglich der einzige Wert ist der die Attraktivität eines Trails bestimmt. Ausgehend von einer Startposition (einem Start-Spot) darf dann jede Ameise zufällig einen Pfad über die Spots suchen, wobei die Entscheidung für einen Trail zwar zufällig ist, jedoch mit einer durch die A-Priori-Werte bestimmten Wahrscheinlichkeit vorgenommen wird.Sind alle Ameisen an ihrem Ziel (wie immer das auch definiert ist) angekommen wird für jede Ameise die Güte ihrer Lösung bestimmt (wobei die Lösung dem gelaufenen Pfad entspricht). Ensprechend dieser Güte darf dann jede Ameise Pheromon auf den Trails ihres Pfades ablegen. Dieser Pheromonwert jedes Trails summiert sich auf, unterliegt jedoch auch einer "Verdunstung", die dafür sorgt, dass sich zwischen zwei Läufen der Pheromonwert jedes Trails jeweils um einen bestimmten Prozentsatz verringert. Für die weiteren Läufe, bei denen alle Ameisen erneut Lösungen suchen, indem sie von ihrer Startposition ausgehend einen Pfad zu der/einer gültigen Zielposition suchen, bestimmt sich die Attraktivität eines Trails neben dem A-Priori-Wert auch durch die Menge des dort abgelegten (und noch nicht verdunsteten) Pheromons. Die Wahrscheinlichkeit am Spot S einen (noch) möglichen Trail Trailx aus der Menge der von S abgehenden Trails zu nehmen ist bestimmt durch:
| P(Trailx|S) = | Prior(Trailx|S)Beta
* Pheromon(Trailx|S)Alpha
|
|||
|
Der Nenner ist dabei eine Normierungskonstante, die durch die Summe der Werte aller noch möglichen von S abgehenden Trails bestimmt wird. Alpha und Beta sind zwei Werte, die die Wichtigkeit des Pheromons bzw. der A-Priori-Werte bestimmen. Diese Formel kann auch für den ersten Lauf verwendet werden, wenn ein initialer Pheromon-Level für all Trails vorgegeben wird. Es existieren verschiedene Abwandlungen und Erweiterungen, die z.B. den Pheromonwert der Trails auf einen minimalen und einen maximalen Wert begrenzen, oder nur der/den beste(n) Ameise(n) des letzten Laufs/aller vorhergehenden Läufe erlauben Pheromon abzulegen. Das Verfahren zeigt zum Beispiel für das Traveling-Salesman-Problem gute Ergebnisse.
In unserem Fall soll die Ameise ja eine Eliminierungsreihenfolge der Knoten finden, d.h. die Spots sind die (zu eliminierenden) Knoten des moralischen Graphen. Zusätzlich wird ein Start-Spot eingeführt, von dem aus alle Ameisen starten und von dem aus jeder andere Spot erreichbar ist, der jedoch selbst keinem Knoten des moralischen Graphen entspricht. Eine Pfadsuche einer Ameise ist beendet sobald sie alle Spots einmal besucht hat, wobei sie keinen Spot zweimal besuchen darf (Trails die dazu führen würden dürfen nicht benutzt werden). Der Pfad ist dann eine Eliminierungsreihenfolge.
Nun ist das Problem, dass es keinen Sinn macht die Ameisen zunächst rein zufällig loslaufen zu lassen, da die Wahrscheinlichkeit hierbei irgendwelche brauchbaren Lösungen zu finden im Allgemeinen so gering ist, dass man nahezu unendlich viele Ameisen (Lösungen) generieren müsste. Andererseits versagt die Möglichkeit die Ameisen durch einen fest an jeden Trail gehängten A-Priori-Wert zu führen, da die Qualität / Güte eines nächsten Spots (zu eliminierenden Knotens) von allen zuvor eliminierten Knoten abhängt. So kann der Pfad A-> B -> C -> D -> E sehr gut sein, während A -> E -> C -> D -> B sehr schlecht ist. Im zweiten Fall kann gerade die Eliminierung von D nach C zu einer besonders schlechten Decomposion führen, während dieselbe Teilreihenfolge im ersten Fall noch besonders gut war. Daher bestimmen die Ameisen den A-Priori-Wert aller von einem Spot S abgehenden Trails selbst durch einen One-Step-Lookahead-Algorithmus sobald sie an diesem Spot S angelangt sind. Leider scheint genau diese Herangehensweise problematisch zu sein, wie die unten gezeigten Grafiken verdeutlichen. Die initiale Lösungsmenge nach dem ersten Lauf entspricht erwartungsgemäß genau dem Spektrum, welches auch ein N mal wiederholter One-Step-Lookahead-Algorithmus liefern würde. Danach folgt eine Phase in der zwar systematisch bessere Lösungen gefunden werden, jedoch treten gleichzeitig auch besonders schlechte Lösungen auf, die sehr viel schlechter sind als die schlechtesten Lösungen der initialen Lösungsmenge des ersten Laufs. Da das Pheromon naturgemäß nicht die Historie des bereits zurückgelegten Pfads berücksichtigt, sondern (so wie normalerweise auch der A-Prior-Wert) fest bestimmten Trails zugeordnet ist, kann es Ameisen offenbar auch schwer in die Irre führen. Danach folgt oft eine Phase in der die Lösungen aller Ameisen gegen ein und dieselbe Lösung konvergieren, also alle Ameisen demselben Pfad folgen, diese Lösung aber relativ schlecht ist. Diese Lösung wird besser wenn nur einem bestimmten Prozentsatz der besten Ameisen erlaubt wird Pheromon abzulegen und zwar umso besser, je kleiner dieser Prozentsatz ist (z.B. nur die besten 5% der Ameisen). Allerdings vergrößert sich damit auch die Gefahr das Optimum zu verpassen und in einem lokalen Minimum hängen zu bleiben. Andererseits lässt sich auch das Zusammenfallen der unterschiedlichen Lösungen, zu nur noch einer einzigen Lösung, mit geeigneten Parametereinstellungen oft verhindert. Das Problem, dass nach der Anfangsphase keine besseren Lösungen mehr gefunden werden bleibt jedoch bestehen. So wird die beste Lösung oft nach wenigen Läufen erreicht, diese ist jedoch bei komplexen Graphen oft noch weit weg vom globalen Optimum...
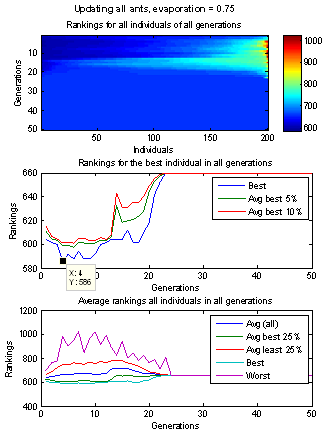
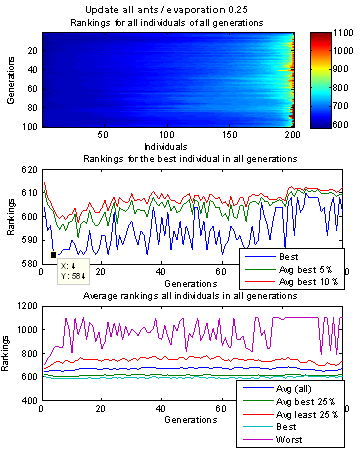
Decomposition mit Ant-Colony-Optimization
Evolutionäre Algorithmen (EA):
Bei evolutionären Algorithmen werden (mehr oder weniger) zufällig eine initiale Menge von Lösungen (Individuen) erzeugt. Durch bestimmte Rekombinations-Operatoren können jeweils zwei Individuen einen oder mehrere Nachkommen erzeugen, welche zusätzlich noch durch Mutations-Operatoren verändert werden können. Die Menge der Individuen einer Generation sowie die Menge aller neu erzeugten Nachkommen bildet die nächste Generation, wobei die (gemäß einer Bewertungsfunktion) schlechtesten Individuen ausgesondert werden, so dass jeweils nur eine vorgegebene Anzahl von Individuen "überlebt". Auf diese Art können gute Individuen viele Generationen lang überleben, während schlechte Nachkommen unmittelbar wieder aus der Population herausfallen.
Folgende Parameter werden definiert:
- Population: eine initiale Menge von Individuen (also den zu optimierenden Objekten)
- Recombinator: ein Operator, der aus zwei Individuen einen Nachkommen erzeugen kann.
- Fitness: ein Operator, der jedem Individuum einen Fitness-Wert zuordnet, der die Güte des Individuums (der Lösung) beschreibt.
- maxGenerations: die maximale Anzahl von Generationen die erzeugt wird
- maxPopulation: die maximale Anzahl von Individuen die gleichzeitig in der Population "leben" dürfen; sind mehr enthalten werden die schlechtesten verworfen ("sterben")
- maxChildren: die maximale Anzahl von neuen Individuen, die durch den Recombinator in einer Generation erzeugt werden (sind dann mehr als maxPopulation Individuen enthalten greift der gerade beschriebene Filter-Mechanisimus)
- aging: ein Offset der in jeder Generation die ein Individuum bereits überlebt hat, auf die Fitness-Bewertungen dieses Individuums addiert wird.
- satisfyingFitness:
wird ein Individuum erzeugt und mit ein Fitness-Wert
bewertet, der mindestens diesen Wert hat, dann wird
die Suche abgebrochen, da ein
ausreichen gutes Individuum gefunden wurde.
- Solange noch nicht maxGenerations erzeugt wurden und
noch kein Individuum mit
mindestens der vorgegebenen satisfyingFitness
gefunden wurde:
- Erhöhe die Bewertung aller Individuen, die derzeit in der Poulation sind um den Wert aging
- Über alle IndividuenI1 der aktuellen Population (beste zuerst):
- Über alle IndividuenI2 der aktuellen Population (beste zuerst):
- benutze den Recombinator um einen Nachkommen I12 aus I1 und I2 zu erzeugen, bewerte ihn mit dem Fitness-Operator und füge I12 der Population hinzu
- Wenn der Recombinator nicht symmetrisch ist, dann erzeuge auch noch einen Nachkommen I21 aus I2 und I1, bewerte auch diesen und füge I21 ebenfalls der Population hinzu
- Wenn bereits maxChildren Nachkommen erzeugt wurden breche ab (ggf. auch schon vor dem zuletzt beschriebenen Schritt)
- Der Mutations-Operator,
der
erzeugte Individuen noch zufälligen
Veränderungen unterwirft, wird
hier als Teil des Recombinators
gesehen,
auch wenn in diesem nicht "fest-verdrahtet" sondern
austauschbar implementiert werden sollte.
- Man kann sich z.B. auch
Meta-Recombinator-Operatoren
vorstellen die selbst nur bei jeder "Paarung" unter
mehreren
verfügbaren Rekombinations-Operatoren einen
auswählen und
anwenden, um so evtl. eine noch größere
Vielfalt an
Individuen zu erzeugen.
Es gibt viele Standard-Rekombinations-
und Mutations-Operatoren
wobei
einige auch speziell für Reihenfolgeprobleme geeignet
sind. Die
Ergebnisse für eine kleine Auswahl dieser Operatoren
sind unten
abgebildet. Die genaue Beschreibung würde den Rahmen
dieser kurzen
Einführung sprengen, kann aber in [2]
nachgelesen werden.
Grundsätzlich zeigen die evolutionären Algorithmen
eine klare
Konvergenz hin zu immer besseren Lösungen, wobei die
Lösungen
auch ganz am Ende i.d.R. noch alle unterschiedlich, wenn
auch alle
(fast)
gleich gut sind. Für hinreichend komplexe Netze sind
die
Lösungen praktisch immer denen mit ACO gefundenen
überlegen.
Die Konvergenzgeschwindigkeit
kann durch stärker spezialisierte
Operatoren z.T. noch erheblich gesteigert werden. Der EOT-Recombinator (siehe
Grafik
unten), der
zwar erheblich mehr Rechenzeit pro Generation erfordert,
dies aber
durch die
schnellere Konvergenz wieder mehr als wettmacht, ist ein
Beispiel
für einen solchen stark spezialisierten Operator. Er
kombiniert
dabei nicht direkt zwei Eliminierungsreihenfolgen, wie die
anderen
erprobten Rekombinations-Operatoren. Stattdessen kombiniert
er die aus
Eliminierungsreihenfolgen resultierenden Strukturen (die
sich ja durch
verschiedene Triangulierungen, also durch ihre
Fill-In-Kanten
unterscheiden), um aus einer "rekombinierten" Struktur
wieder eine neue
Eliminierungsreihenfolge abzuleiten (z.B. mithilfe eines 1-Step-Lookahead-Verfahrens).
Der folgende Kasten erläutert den Algorithmus im
Detail:
Folgende Parameter werden definiert:
- pSuccess:
die Wahrscheinlichkeit, dass zwei Eltern-Individuen
in einer Generation
überhaupt ein Kind generieren (ein allgemeiner
Parameter, den alle
Recombinator-Operatoren haben)
- pTakeFrom1:
die Wahrscheinlichkeit, dass eine Fill-In-Kante
übernommen wird,
die nur in genau einem Eltern-Individuum vorkommt
(der optimale Wert
hierfür scheint zumeist bei 0 zu liegen, so
dass dieser Parameter
auch weggelassen werden kann und entsprechend
niemals Fill-Ins
übernommen werden, die nur in einem
Eltern-Inidividuum vorkommen)
- pTakeFrom2:
die Wahrscheinlichkeit, dass eine Fill-In-Kante
übernommen wird,
die in beiden Eltern-Individuen vorkommt (der
optimale Wert
hierfür scheint zumeist bei 1, oder zumindest
sehr nahe an 1 zu
liegen, so dass auch dieser Wert nicht zwingend
parametrisierbar
gehalten werden muss und solche Fill-Ins immer
übernommen werden
können)
- Mutator:
der
Mutations-Operator, der auf der erzeugten
Elimination-Order noch
Veränderungen machen darf6)
- Ein Rauschen, welches die Bewertung eines Knotens bei der Frage, welcher Knoten als nächstes eliminiert werden soll beeinflusst.
- maxFillIns:
eine maximal erlaubte Anzahl von Fill-Ins bei deren
Überschreitung
abgebrochen und letztlich kein Nachkomme erzeugt
wird.
- Erzeuge einen zufälligen Wert zwischen 0 und
1 -
wenn dieser kleiner pSuccess ist,
brich ab und liefere keinen Nachkommen zurück
(wenn man sicherstellen
will, dass tatsächlich mit genau dieser
Wahrscheinlichkeit ein Nachkommen-Individuum erzeugt
wird, kann man
diese Prüfung nicht bereits hier am Anfang,
sondern - in
modifizierter
Form - erst am Ende machen, wenn man sicher ist,
dass der Algorithmus
nicht aus anderen Gründen abgebrochen wurde -
z.B. wegen zu vieler
Fill-Ins)
- Erzeuge ein Netz mit denselben Kanten wie sie im
Ursprungsnetz enthalten waren (ohne Fill-Ins)7)
- Übernehme in dieses Netz von beiden Eltern-Netzen die Fill-In-Kanten entsprechend den Wahrscheinlichkeiten pTakeFrom1 und pTakeFrom2
- Benutze einen 1-Step-Lookahead-Algorithmus (ggf.
mit
verrauschten Knoten-Bewertungen, s.o.) um eine
Eliminierungsreihenfolge
und zusätzlich nötige Fill-Ins für
das erzeugte
Nachkommen-Netz zu bestimmen (theoretisch kan hier
auch ein anderer
Optimierungs-Algorithmus als 1-SLAT benutzt werden,
nur sollte er
möglichst performant sein)
- Wende den Mutator auf diese Eliminierungsreihenfolge an.
- Wenn der Mutator die Eliminierungsreihenfolge noch verändert hat, dann verwerfe das Nachkommen-Netz und benutze erneut einen 1-Step-Lookahead-Algorithmus um ausgehend vom Originalnetz (ohne Fill-Ins!), die Triangulierung und damit die entsprechenden Fill-Ins, gemäß der mutierten Eliminierungsreihenfolge, für das Nachkommen-Netz zu bestimmen
- Gib das erzeugte Netz als Nachkommen der beiden
Ausgangsnetze (Individuen) zurück.
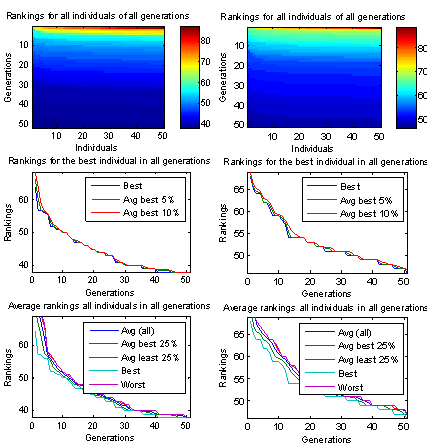
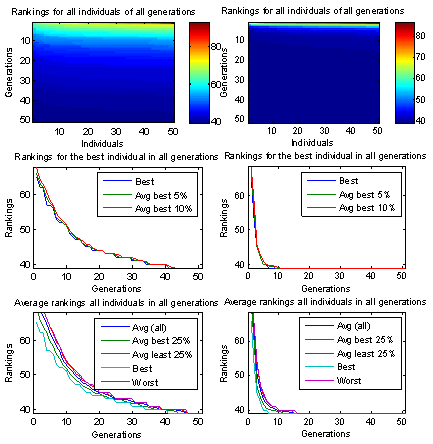
Decomposition mit Evolutionären Algorithmen